10 листопада.
Текст самостійної роботи.
Підготовка до контрольної роботи.
Виконайте всі завдання, крім № 1 та № 3
Метод інтервалів
1. Схема розв’язування нерівності
методом інтервалів :
1. Привести нерівність до такого виду, де в
лівій частині знаходиться функція, а в правій 0.
2. Знайти область визначення функції.
3. Знайти нулі функції, тобто розв’язати
рівняння f(x)=0
4. На числову пряму нанесемо область
визначення функції і за допомогою нулів розіб’ємо її (область визначення) на
інтервали.
5. Визначити знаки функції на отриманих
інтервалах.
6. Вибрати інтервали, де функція набуває
необхідних значень і записати відповідь.
Приклад Розв'язати нерівність (x-3)(x+5)(4-x)≥0.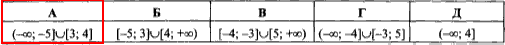
Обчислення: Такі нерівності розв'язують методом інтервалів.
Суть методу полягає в нанесенні всіх точок в порядку зростання на числову вісь. Далі визначаємо знак функції в одному з інтервалів. В усіх наступних вони будуть чергуватися "мінус, плюс, мінус".
Виняток становлять кратні корені, це наприклад вирази в парних степенях. При переході через такі точки функція не змінює знаку.
Зараз Ви це все побачите з наступних тестових завдань.
Винесемо -1 з останніх дужок і помножимо цю нерівність на -1:
-1•(x-3)(x+5)(x-4)≥0, отже
(x-3)(x+5)(x-4)≤0 (знак нерівності змінили!)
Розв'яжемо відповідне рівняння:
(x-3)(x+5)(x-4)=0, звідси отримаємо x1=3, x2=-5 і x3=4.
Нанесемо їх на числову пряму і побудуємо інтервали.
Підстановкою точки x=0 перевіряємо знак на проміжку [-5;3], на сусідніх знаки чергуються.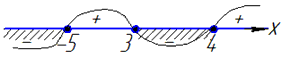
Оскільки тепер a>0 то починаємо будувати інтервали над віссю Ox, (для a<0 треба було б починати з «-», тобто будувати під віссю Ox);
так як знак нерівності «менше (або дорівнює) нулю», то беремо у відповідь ті інтервали, у яких крива знаходиться під віссю Ox (і на осі Ox), тобто
x∈(-∞;-5]∪[3;4].
Відповідь:А.
Для самостійної роботи виконайте вправи 5.1, 5.3, 5.5 вашого підручника.




Немає коментарів:
Дописати коментар