Повторення вивченого матеріалу з математики здійснюється для підготовки до написання річної підсумкової контрольної роботи. Збірник завдань з математики допоможе вам у цій підготовці. Учні 9-х класів уже почали таку роботу в ІІ семестрі.
Повторення: декартові координати на площині.
Повторення: розв'язування систем рівнянь.
Схема розвязування систем рівнянь
Графічний метод
- Виконуємо рівносильні перетворення, так, щоб було зручно побудувати графік функції. Наприклад:
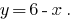
- Будуємо графіки.
- Знаходимо точки перетину графіків. Координати цих точок і є розв'язком даної системи рівнянь.
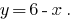
Метод підстановки
- З одного рівняння системи виражаємо одну змінну через іншу, завжди обираємо зручну змінну. Наприклад, з рівняння
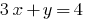виражаємо змінну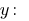 
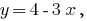а не навпаки.
- Знайдене значення підставляємо у інше рівняння системи, і одержуємо рівняння з однією змінною.
- Розв'язуємо одержане рівняння
- Знайдене значення підставляємо у виражене рівняння, і знаходимо значення другої змінної.
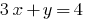виражаємо змінну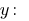 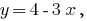а не навпаки.Метод додавання
- Урівнюємо коефіцієнти при одній зі змінних шляхом почленного множення обох рівнянь на множники, підібрані відповідним чином.
- Додаємо (або віднімаємо) почленно два рівняння системи, тим чином виключається одна змінна.
- Розв'язуємо одержане рівняння.
- Підставляємо знайдене значення змінної у будь-яке з вихідних рівнянь.
Повторення: перетворення раціональних виразів
Повторення: вписані та описані чотирикутники
Повторення: чотирикутники.
Чотирикутником називають фігуру, яка складається з чотирьох точок і чотирьох відрізків, які послідовно їх сполучають.
Ніякі три з даних точок не повинні лежати на одній прямій, а відрізки, які їх сполучають, не повинні мати ніяких інших спільних точок крім даних.
На малюнку 233 зображено чотирикутник АВСD. Точки А, В, С, D називають вершинами чотирикутника, а відрізки АВ, ВС, СD і DА, що їх сполучають, - сторонами чотирикутника.
Вершини чотирикутника, які є кінцями однієї його сторони, називають, сусідніми, несусідні вершини називають протилежними.
На малюнку 233 вершини А і В - сусідні, А і С - протилежні. Відрізки, які сполучають протилежні вершини чотирикутника, називають діагоналями чотирикутника. На малюнку 234 відрізки КМ і LN - діагоналі чотирикутника КLМN. Будь-який чотирикутник має дві діагоналі.
Сторони чотирикутника, які мають спільну вершину, називають сусідніми, а які не мають спільної вершини, - протилежними. На малюнку 233 сторони АВ і ВС - сусідні, сторони АВ і СD - протилежні.
Суму довжин усіх сторін чотирикутника називають його периметром. Периметр позначають буквою Р.
Наприклад, периметр чотирикутника АВСD можна позначити так: РАВСD. Маємо РАВСD = АВ + ВС + СD + DА.
Кутами чотирикутника ABCD називають кути DAB, ABC, BCD і CDA (мал. 233). Кути чотирикутника називають протилежними, якщо їх вершини - протилежні вершини чотирикутника, і сусідніми, якщо їх вершини - сусідні вершини чотирикутника. На малюнку 233 кути А і С - протилежні; А і В - сусідні.
Один з кутів чотирикутника може бути більшим від розгорнутого. Наприклад, на малюнку 235 кут А чотирикутника ABCD більший за розгорнутий. Такий чотирикутник називають неопуклим. Якщо ж усі кути чотирикутника менші від 180°, то його називають опуклим. Сума кутів чотирикутника дорівнює 360°.
Приклад. Знайдіть невідомі кути чотирикутника, якщо один з них дорівнює 120°, другий та третій відносяться, як 3:5, а четвертий дорівнює півсумі другого та третього.
Розв’язання. Нехай у чотирикутнику АВСВ: 
A = 120°. За умовою B : C = 3 : 5. Можна позначити B = 3х; C = 5х.
Тоді 
Маємо рівняння 
Тоді 
A = 120°. За умовою B : C = 3 : 5. Можна позначити B = 3х; C = 5х. Тоді
Означення паралелограма та його властивості.
Паралелограмом називають чотирикутник, у якого протилежні сторони попарно паралельні.
На малюнку 236 зображено паралелограм АВСD: АВ || СD, АD || ВС.
Розглянемо властивості паралелограма:
1) Сума будь-яких двох сусідніх кутів паралелограма дорівнює 180°.
2) Паралелограм є опуклим чотирикутником.
3) У паралелограмі протилежні сторони рівні, протилежні кути рівні.
На малюнку 236: АВ = СD, АD = ВС, A = C, B = D.
4) Периметр паралелограма РАBCD = 2(АВ + ВС).
5) Діагоналі паралелограма перетинаються і точкою перетину діляться пополам.
На малюнку 237: точка О - точка перетину діагоналей паралелограма; АО = ОС; ВО = ОD.
6) Сума квадратів діагоналей паралелограма дорівнює сумі квадратів усіх його сторін.
На малюнку 234: 
Приклад 1. Знайдіть усі кути паралелограма, якщо сума двох з них дорівнює 140°.
Розв’язання. Оскільки сума двох кутів паралелограма дорівнює 140°, то це - протилежні кути, наприклад A і C на малюнку 236. Оскільки A = C, то
Приклад 2. У паралелограмі АВСВ бісектриса кута А ділить сторону ВС на відрізки ВК = 3 см і КС = 2 см (мал. 238). Знайдіть периметр паралелограма.
Розв’язання.
1) ВС = ВК + КС = 3 + 2 = 5 (см).
2) KAD = ВКА (як внутрішні різносторонні кути при перетині паралельних прямих АВ і ВС січною АК).
3) KAD = КАВ (за умовою), тому ВКА = КАВ. Отже, за ознакою рівнобедреного трикутника: ∆АВК - рівнобедрений, АВ = ВК = 3 см.
4) PABCD = 2(AB + ВС) = 2(3 + 5) = 16 (см).
Приклад 3. Діагоналі паралелограма дорівнюють 7 см і 12 см, а одна із сторін на 1 см менша за другу. Знайдіть сторони паралелограма.
Розв’язання (мал. 237). 1) За умовою АС = 11 см; ВD = 7 см. Нехай АD = х см, тоді ВС = (х - 1) см.
2) За властивістю діагоналей паралелограма маємо: 
Враховуючи х > 0, маємо х = 7. Отже, АD = 7 см, ВС = 6 см.
Висотою паралелограма називають перпендикуляр, проведений з будь-якої точки сторони паралелограма до прямої, що містить протилежну сторону.
На малюнку 239 MN - висота паралелограма; МN 
АD, ММ ВС.
З кожної вершини паралелограма можна провести дві висоти. Наприклад, на малюнку 240 ВF і ВТ - висти паралелограма, проведені відповідно до сторін АD і СD.
Приклад 4. У паралелограмі ABCD з вершини тупого кута В проведено висоти BF і ВТ (мал. 240), FBT = 65°. Знайдіть кут А паралелограма.
Розв’язання. 1) У чотирикутнику FBTD: D = 360° - (65° + 2 ∙ 90°) = 115°.
2) Тоді A = 180° - D = 180° - 115° = 65°.
A = C, B = D.A і C на малюнку 236. Оскільки A = C, тоKAD = ВКА (як внутрішні різносторонні кути при перетині паралельних прямих АВ і ВС січною АК).KAD = КАВ (за умовою), тому ВКА = КАВ. Отже, за ознакою рівнобедреного трикутника: ∆АВК - рівнобедрений, АВ = ВК = 3 см. АD, ММ ВС.FBT = 65°. Знайдіть кут А паралелограма.D = 360° - (65° + 2 ∙ 90°) = 115°.A = 180° - D = 180° - 115° = 65°.
Ознаки паралелограма.
Якщо у чотирикутнику:
1) дві сторони паралельні і рівні, або
2) протилежні сторони попарно рівні, або
3) діагоналі перетинаються і точкою перетину діляться пополам, або
4) протилежні кути попарно рівні, то чотирикутник є паралелограмом.
Приклад. У чотирикутнику ABCD (мал. 241) AD = ВС, CAD = ACB, АВ = 3 см. Знайдіть CD та визначте вид чотирикутника ABCD.
Розв’язання. 1) АС – спільна сторона ∆CAD і ∆АСВ.
2) Маємо: ∆CAD = ∆АСВ (за двома сторонами і кутом між ними). Тому CD = АВ = 3 см.
3) У чотирикутнику ABCD протилежні сторони попарно рівні, тому він є паралелограмом.
Прямокутник
Прямокутником називають паралелограм, у якого всі кути прямі (мал. 242).
Розглянемо властивості прямокутника:
1) У прямокутнику протилежні сторони попарно рівні.
На малюнку 242: АВ = СD, АD = ВС.
2) Периметр прямокутника РАВCD = 2(АВ + ВС).
3) Діагоналі прямокутника рівні і точкою перетину діляться пополам.
На малюнку 243: АС = ВD і АО = ОС, ВО = DО. Оскільки АС = ВD, то матимемо АО = ВО = СО = DО. Тому маємо наступну властивість.
4) Точка перетину діагоналей прямокутника рівновіддалена від усіх його вершин.
5) Приклад 1. Діагональ прямокутника ділить його кут у відношенні 4:5. Знайдіть кут між діагоналями даного прямокутника.
Розв’язання. 1) (мал. 243). Нехай АDО : ОDС = 4 : 5. Позначимо АDО = 4х, ОDС = 5х. Тоді 4х + 5х = 90°; х = 10°. Тому АDО = 4 ∙ 10° = 40°; ОDС = 5 ∙ 10° = 50°.
2) ∆ОСD - рівнобедрений (бо ОD = ОС). Тому ОСD = ОDС = 50°. У ∆ОСD: ОСD = 180° - 2 ∙ 50° = 80°. Отже, кут між діагоналями даного прямокутника дорівнює 80°.
Приклад 2. У прямокутнику АВСD діагоналі перетинаються в точці О. ОР - бісектриса трикутника АОВ, DОР = 160°. Знайдіть САВ.
Розв’язання (мал. 244).
1) РОВ = 180° - 160° = 20°.
2) Оскільки ОР - бісектриса ∆АОВ, то ВОА = 2 ∙ 20° = 40°.
3) ∆АОВ - рівнобедрений (бо АО = ОВ), тому 
Приклад 3. Периметр прямокутника дорівнює 34 см, а його діагональ 13 см. Знайдіть сторони прямокутника.
Розв’язання. 1) Нехай сторони прямокутника дорівнюють а см і b см.
Тоді 2(а + b) = 34, тобто а + b = 17 і 
2) Маємо систему
Отже, сторони прямокутника дорівнюють 5 см і 12 см.
Ознаки паралелограма.
Якщо у чотирикутнику:
1) дві сторони паралельні і рівні, або
2) протилежні сторони попарно рівні, або
3) діагоналі перетинаються і точкою перетину діляться пополам, або
4) протилежні кути попарно рівні, то чотирикутник є паралелограмом.
Приклад. У чотирикутнику ABCD (мал. 241) AD = ВС, CAD = ACB, АВ = 3 см. Знайдіть CD та визначте вид чотирикутника ABCD.
CAD = ACB, АВ = 3 см. Знайдіть CD та визначте вид чотирикутника ABCD.
Розв’язання. 1) АС – спільна сторона ∆CAD і ∆АСВ.
2) Маємо: ∆CAD = ∆АСВ (за двома сторонами і кутом між ними). Тому CD = АВ = 3 см.
3) У чотирикутнику ABCD протилежні сторони попарно рівні, тому він є паралелограмом.
Прямокутник
Прямокутником називають паралелограм, у якого всі кути прямі (мал. 242).
Розглянемо властивості прямокутника:
1) У прямокутнику протилежні сторони попарно рівні.
На малюнку 242: АВ = СD, АD = ВС.
2) Периметр прямокутника РАВCD = 2(АВ + ВС).
3) Діагоналі прямокутника рівні і точкою перетину діляться пополам.
На малюнку 243: АС = ВD і АО = ОС, ВО = DО. Оскільки АС = ВD, то матимемо АО = ВО = СО = DО. Тому маємо наступну властивість.
4) Точка перетину діагоналей прямокутника рівновіддалена від усіх його вершин.
5) Приклад 1. Діагональ прямокутника ділить його кут у відношенні 4:5. Знайдіть кут між діагоналями даного прямокутника.
Розв’язання. 1) (мал. 243). Нехай АDО : ОDС = 4 : 5. Позначимо АDО = 4х, ОDС = 5х. Тоді 4х + 5х = 90°; х = 10°. Тому АDО = 4 ∙ 10° = 40°; ОDС = 5 ∙ 10° = 50°.
АDО : ОDС = 4 : 5. Позначимо АDО = 4х, ОDС = 5х. Тоді 4х + 5х = 90°; х = 10°. Тому АDО = 4 ∙ 10° = 40°; ОDС = 5 ∙ 10° = 50°.
2) ∆ОСD - рівнобедрений (бо ОD = ОС). Тому ОСD = ОDС = 50°. У ∆ОСD: ОСD = 180° - 2 ∙ 50° = 80°. Отже, кут між діагоналями даного прямокутника дорівнює 80°.
ОСD = ОDС = 50°. У ∆ОСD: ОСD = 180° - 2 ∙ 50° = 80°. Отже, кут між діагоналями даного прямокутника дорівнює 80°.
Приклад 2. У прямокутнику АВСD діагоналі перетинаються в точці О. ОР - бісектриса трикутника АОВ, DОР = 160°. Знайдіть САВ.
DОР = 160°. Знайдіть САВ.
Розв’язання (мал. 244).
1) РОВ = 180° - 160° = 20°.
РОВ = 180° - 160° = 20°.
2) Оскільки ОР - бісектриса ∆АОВ, то ВОА = 2 ∙ 20° = 40°.
ВОА = 2 ∙ 20° = 40°.
3) ∆АОВ - рівнобедрений (бо АО = ОВ), тому
Приклад 3. Периметр прямокутника дорівнює 34 см, а його діагональ 13 см. Знайдіть сторони прямокутника.
Розв’язання. 1) Нехай сторони прямокутника дорівнюють а см і b см.
Тоді 2(а + b) = 34, тобто а + b = 17 і
2) Маємо систему
Отже, сторони прямокутника дорівнюють 5 см і 12 см.
Ознаки прямокутника.
Якщо у паралелограма:
1) всі кути рівні, або
2) один кут прямий, або
3) діагоналі рівні, то паралелограм є прямокутником.
Приклад. У колі з центром О проведено діаметри АС і ВD (мал. 246). Визначте вид чотирикутника АВСD.
Розв’язання. 1) Оскільки АО = ОС, ВО = ОD (як радіуси), то, за ознаками паралелограма, маємо, що АВСD - паралелограм.
2) Оскільки АС = ВD (як діаметри), то використовуючи ознаку прямокутника, маємо, що паралелограм АВСD є прямокутником.
Ромб та його властивості.
Ромбом називають паралелограм, у якого всі сторони рівні (мал. 247).
Розглянемо властивості ромба:
1) Сума будь-яких двох сусідніх кутів ромба дорівнює 180°.
2) У ромба протилежні кути рівні.
На малюнку 247: A = C; B = D.
3) Діагоналі ромба перетинаються і точкою перетину діляться пополам.
На малюнку 248: АО = ОС; ВО = ОD.
4) Периметр ромба РАВCD = 4 ∙ АD.
5) Діагоналі ромба взаємно перпендикулярні.
На малюнку 248: АС 
ВD.
6) Діагоналі ромба ділять кути ромба пополам.
Враховуючи цю властивість і властивість 2 можна зауважити, що 
Приклад 1. Периметр ромба на 15 см більший за його сторону. Знайдіть сторону ромба.
Розв’язання. Нехай сторона ромба дорівнює а см, тоді його периметр дорівнює 4а см. За умовою 4а - а = 15; 3а = 15; а = 5 (см). Отже, сторона ромба дорівнює 5 см.
Приклад 2. ABCD - ромб, 2 = 70°. (мал. 249). Знайдіть 1.
Розв’язання.
Приклад 3. ABCD - ромб, 1 = 50°. (мал. 249). Знайдіть 3.
Розв’язання. 
- внутрішні різносторонні. Тому 3 = 2 = 80° .
Приклад 4. Кут між висотою і діагоналлю ромба, проведеними з однієї вершини і дорівнює 26°. Знайдіть гострий кут ромба.
Розв’язання. 1) BD - діагональ ромба ABCD, ВК - його висота (мал. 250), KBD = 26° (за умовою).
2) У ∆BKD BDK = 90° – 26° = 64°.
3) ADC = 2 ∙ 64° = 128°. Тоді BAD = 180° - 128° = 52°. Отже, гострий кут ромба дорівнює 52°.
Ознаки ромба.
Якщо у паралелограма:
1) дві сусідні сторони рівні, або
2) діагоналі перетинаються під прямим кутом, або
3) діагональ ділить навпіл кут паралелограма, то паралелограм є ромбом.
Приклад. Всі сторони чотирикутника рівні. Встановіть вид чотирикутника.
Розв’язання. 1) Нехай АВ = ВС = СD = DА (мал. 247). Оскільки у чотирикутника протилежні сторони попарно рівні, то за означенням паралелограма, маємо, що АВСD - паралелограм.
2) У паралелограма АВСD сусідні сторони рівні. Тому АВСD - ромб (за ознакою ромба).
Квадрат та його властивості.
Квадратом називають прямокутник, у якого всі сторони рівні (мал. 251).
Сформулюємо властивості квадрата:
1) Усі кути квадрата прямі.
2) PABCD = 4 ∙ AВ (мал. 251).
3) Діагоналі квадрата рівні.
На малюнку 252: АС = BD.
4) Діагоналі квадрата перпендикулярні і точкою перетину діляться пополам.
На малюнку 252: АС BD і АО = ВО = CO = DO (враховуючи властивість 3).
5) Діагоналі квадрата ділять його кути пополам, тобто утворюють зі сторонами квадрата кути 45°.
Приклад 1. Точка перетину діагоналей квадрата віддалена від його сторони на 5 см. Знайдіть периметр квадрата.
Розв’язання. 1) Нехай точка О - точка перетину діагоналей квадрата ABCD (мал. 253). OK AD, OK = 5 см - відстань від точки О до сторони квадрата AD.
2) ОК - висота рівнобедреного трикутника AOD (у якого АО = OD), тому вона також медіана і бісектриса.
3) Оскільки 
то ∆АОК - рівнобедрений АК = КО = 5 см. Аналогічно KD = 5 см.
4) Сторона ромба АD = 5 ∙ 2 = 10 (см), його периметр Р = 10 ∙ 4 = 40 (см).
Приклад 2. У рівнобедрений прямокутний трикутник АВС (C = 90°) вписано квадрат CMNK так, що прямий кут у трикутника і квадрата спільний, а точка N належить АВ. Периметр квадрата дорівнює 40 см. Знайдіть довжину катета трикутника.
Розв’язання. 1) На малюнку 254 квадрат СМNК вписано у ∆АВС вказаним способом.
3) A = 45°. В ∆AMN: ANM = 90° - 45° = 45°. Тому ∆AMN - рівнобедрений і AM = MN = 10 (см).
4) Тоді катет трикутника АС = СМ + МА = 10 + 10 = 20 (см).
Ромб та його властивості.
Ромбом називають паралелограм, у якого всі сторони рівні (мал. 247).
Розглянемо властивості ромба:
1) Сума будь-яких двох сусідніх кутів ромба дорівнює 180°.
2) У ромба протилежні кути рівні.
На малюнку 247: A = C; B = D.
A = C; B = D.
3) Діагоналі ромба перетинаються і точкою перетину діляться пополам.
На малюнку 248: АО = ОС; ВО = ОD.
4) Периметр ромба РАВCD = 4 ∙ АD.
5) Діагоналі ромба взаємно перпендикулярні.
На малюнку 248: АС ВD.
ВD.
6) Діагоналі ромба ділять кути ромба пополам.
Враховуючи цю властивість і властивість 2 можна зауважити, що
Приклад 1. Периметр ромба на 15 см більший за його сторону. Знайдіть сторону ромба.
Розв’язання. Нехай сторона ромба дорівнює а см, тоді його периметр дорівнює 4а см. За умовою 4а - а = 15; 3а = 15; а = 5 (см). Отже, сторона ромба дорівнює 5 см.
Приклад 2. ABCD - ромб, 2 = 70°. (мал. 249). Знайдіть 1.
2 = 70°. (мал. 249). Знайдіть 1.
Розв’язання.
Приклад 3. ABCD - ромб, 1 = 50°. (мал. 249). Знайдіть 3.
1 = 50°. (мал. 249). Знайдіть 3.
Розв’язання.
- внутрішні різносторонні. Тому 3 = 2 = 80° .
Приклад 4. Кут між висотою і діагоналлю ромба, проведеними з однієї вершини і дорівнює 26°. Знайдіть гострий кут ромба.
Розв’язання. 1) BD - діагональ ромба ABCD, ВК - його висота (мал. 250), KBD = 26° (за умовою).
KBD = 26° (за умовою).
2) У ∆BKD BDK = 90° – 26° = 64°.
BDK = 90° – 26° = 64°.
3) ADC = 2 ∙ 64° = 128°. Тоді BAD = 180° - 128° = 52°. Отже, гострий кут ромба дорівнює 52°.
ADC = 2 ∙ 64° = 128°. Тоді BAD = 180° - 128° = 52°. Отже, гострий кут ромба дорівнює 52°.
Ознаки ромба.
Якщо у паралелограма:
1) дві сусідні сторони рівні, або
2) діагоналі перетинаються під прямим кутом, або
3) діагональ ділить навпіл кут паралелограма, то паралелограм є ромбом.
Приклад. Всі сторони чотирикутника рівні. Встановіть вид чотирикутника.
Розв’язання. 1) Нехай АВ = ВС = СD = DА (мал. 247). Оскільки у чотирикутника протилежні сторони попарно рівні, то за означенням паралелограма, маємо, що АВСD - паралелограм.
2) У паралелограма АВСD сусідні сторони рівні. Тому АВСD - ромб (за ознакою ромба).
Квадрат та його властивості.
Квадратом називають прямокутник, у якого всі сторони рівні (мал. 251).
Сформулюємо властивості квадрата:
1) Усі кути квадрата прямі.
2) PABCD = 4 ∙ AВ (мал. 251).
3) Діагоналі квадрата рівні.
На малюнку 252: АС = BD.
4) Діагоналі квадрата перпендикулярні і точкою перетину діляться пополам.
На малюнку 252: АС BD і АО = ВО = CO = DO (враховуючи властивість 3).
BD і АО = ВО = CO = DO (враховуючи властивість 3).
5) Діагоналі квадрата ділять його кути пополам, тобто утворюють зі сторонами квадрата кути 45°.
Приклад 1. Точка перетину діагоналей квадрата віддалена від його сторони на 5 см. Знайдіть периметр квадрата.
Розв’язання. 1) Нехай точка О - точка перетину діагоналей квадрата ABCD (мал. 253). OK AD, OK = 5 см - відстань від точки О до сторони квадрата AD.
AD, OK = 5 см - відстань від точки О до сторони квадрата AD.
2) ОК - висота рівнобедреного трикутника AOD (у якого АО = OD), тому вона також медіана і бісектриса.
3) Оскільки то ∆АОК - рівнобедрений АК = КО = 5 см. Аналогічно KD = 5 см.
то ∆АОК - рівнобедрений АК = КО = 5 см. Аналогічно KD = 5 см.
4) Сторона ромба АD = 5 ∙ 2 = 10 (см), його периметр Р = 10 ∙ 4 = 40 (см).
Приклад 2. У рівнобедрений прямокутний трикутник АВС (C = 90°) вписано квадрат CMNK так, що прямий кут у трикутника і квадрата спільний, а точка N належить АВ. Периметр квадрата дорівнює 40 см. Знайдіть довжину катета трикутника.
C = 90°) вписано квадрат CMNK так, що прямий кут у трикутника і квадрата спільний, а точка N належить АВ. Периметр квадрата дорівнює 40 см. Знайдіть довжину катета трикутника.
Розв’язання. 1) На малюнку 254 квадрат СМNК вписано у ∆АВС вказаним способом.
3) A = 45°. В ∆AMN: ANM = 90° - 45° = 45°. Тому ∆AMN - рівнобедрений і AM = MN = 10 (см).
A = 45°. В ∆AMN: ANM = 90° - 45° = 45°. Тому ∆AMN - рівнобедрений і AM = MN = 10 (см).
4) Тоді катет трикутника АС = СМ + МА = 10 + 10 = 20 (см).
Ознаки квадрата.
1) Якщо діагоналі прямокутника перпендикулярні, то він є квадратом.
2) Якщо діагоналі ромба рівні, то він є квадратом.
Приклад. У чотирикутника всі сторони рівні всі кути рівні. Визначте вид чотирикутника.
Розв’язання. 1) Оскільки у чотирикутника всі кути рівні, то за ознакою прямокутника, він є прямокутником.
2) Оскільки у прямокутника всі сторони рівні, то він є квадратом.
12 березня дев'ятикласники отримали завдання розв'язувати варіанти 19, 20, 21.
19 березня школярі напишуть самостійну роботу.
Скан-копії або фото-копії виконаних робіт надсилайте на мою поштову скриньку sh52003@ukr.net
Результати самостійних робіт з аналізом помилок отримаєте індивідуально через електронну пошту
Повторення продовжуємо. Розв'язуйте, будь ласка, варіанти №22, 23, 24, 25.
Немає коментарів:
Дописати коментар